近半个世纪以来, 供暖蒸汽流量计因其测量精度高、 无可动部件、测量精度高等优点得到了迅猛的发展。 供暖蒸汽流量计主要测量部件为压电传感器,其易受到噪声的干扰,如管道振动、电磁干扰、流体的低频摆动等。 在含有噪声的信号的中提取出有用的涡街信号, 国内外众多研究学者对涡街信号的处理方式主要有FFT 的周期图法、互相关法、自适应陷波滤波法、小波分析法和数字跟踪滤波方法等 。 但是这些方法对于含有强噪声的信号测量精度不高或错误,即噪声频率在涡街信号频率范围内,而噪声的幅值高于涡街信号的幅值。 本文提出一种基于稀疏傅里叶变换的涡街信号分析方法, 该方法不仅具有很高的实时性而且对含有强噪声的信号也能够保证测量的准确性。
1 稀疏傅里叶变换的理论分析
快速傅里叶变换( Fast Fourier Transform , FFT )的时间复杂度为 O ( nlogn ),与离散傅里叶变换( Discrete Fourier Trans-form , DFT )的复杂度 O ( N 2 )相比,运算速度发生了质的飞跃,尤其是随着采样点数 N 的增加这种优势就越加明显 。但是随着时代的发展,需要实时处理的信号越来越多,即便是 FFT 对于这样的需求也难以满足。 传统的 FFT 只考虑到了信号的长度 N 需要为 2 的整数次幂,并未考虑到信号的自身的特性,如稀疏性。
在实际生活中常见的信号的傅里叶系数只有小部分是我们感兴趣的,其大部分都是可以忽略的,如图像和语音信号 。 针对这样的信号能否找到一种更加快速的算法来计算其傅里叶变换,MIT的团队给出了答案 。 该团队提出了稀疏傅里叶变换( Sparse Fourier Transform , SFT ), 该算法利用了信号频域的稀疏性,先对信号进行分“桶”,将长的 DFT 运算变为较短的运算,再根据一定的规则重构了信号的频谱,其运算速度为 FFT 的十倍甚至百倍 。
稀疏傅里叶变换使用的先决条件就是分析的信号具有稀疏性,设 x ( n )是长度为 N 点的有限长序列,则该序列的 N 点离散傅里叶变换逆变换为:

其中 Ω N 表示集合 邀0 , 1 ,……, N-1妖 。 只有 K ( K垲N )个非零的傅里叶系数,只通过信号 x ( n )的部分采样值来确定这 K 非零傅里叶系数与位置。
1.1 频域降采样
参数 B 整除 N ,若想要以等间隔 N/B 对信号频域进行降采样,即:

混叠后频域谱线由 N 减少到 B ,信号点数成倍较少,这正是SFT 算法复杂度为亚线性的关键原因之一。
1.2 稀疏傅里叶变换运算步骤
稀疏傅里叶变换包括频谱重排、加窗函数、频域降采样、定位、估值与迭代等运算过程。
1.2.1 频谱重排
频谱重排的目的是使各大值点均匀分布, 分桶时大频点不要分到同一个桶中,当两个或两个以上大值点在同一桶中时,无法求解取大值点的频率和位置。p ( n ) =x { mod [ σ · n , N ]}, nε [ 1 , N ] ( 4 )式中 σ 为一个随机数,且为奇数,并满足 mod [ σ×σ -1 , N ] =1 ,这就保证了 σ 与 N 互为质数, σ -1 为 σ 的模逆算子。 根据傅里叶变换可知上式中的 p ( n ), x ( n )满足:P ( k ) =X { mod [ σ-1 · k , N ]}, σ , kε [ 1 , N ] ( 5 )通过式( 4 )、( 5 )知道信号时域上的重排也会导致频谱信号位置上发生变换。
1.2.2 窗函数滤波器
为了保证算法的效率且防止频谱泄漏,需要设计一个在时域和频域能量都集中的滤波器, 根据文献该滤波器的为 sinc 窗函数与高斯窗函数的卷积,该窗函数具有过渡带陡峭、通带平滑等特点。
1.2.3 哈希映射
定义一个映射区间 Ω N →Ω B 的哈希函数: h σ ( k ) =round ( σ ·k · N/B ), round 表示四舍五入, 将 Ω N 中每一个点都映射到 Ω B中。 定义偏移量: o σ ( k ) =σ · k-h σ ( k )·( N/B );定义集合 J ,集合 J包含了 Z ( k 中 K 个较大幅值的坐标 k ;通过哈希反映射得到 I r ,即 I r =邀kε [ 0 , N-1 ] |h σ ( k ) εJ妖 ,*后从中取出 K 个大值点对原信号的频率估计。
1.2.4 循环投票
对于每一个 kεI , X‘( k ) =Z ( h σ ( k ) W Nτk/G ( o σ ( k ))频率估计值。 每一次定位循环得到一个坐标集合 I r ,在 L=O ( log 2 N )次循环中,对任意坐标 kεI=I 1 U …… υI r ,若出现次数大于 L/2 ,则将其归入集合 I‘ 中,并认为集合 I‘ 包含所有目标频点坐标。 对每一个kεI‘ ,取 L 次循环得到 X ( k )的中值作为*终的频率值,即:X ( k ) =median ( 邀X r ( k ) |rε邀1 ,……, L)
2 涡街信号的特点
在一定范围内,流体流速 V 与涡街频率 f 有以下关系:
f=πK 1 VD2/4 ( 6 )
其中 K 1 为仪表系数, D 为管道直径。在管道口径 D 不变,流体密度不变的情况下,涡街传感器的输出幅值与 f 2 成正比,具体表达形式可以根据实验测出。本文以 50mm 口径气体实验为例,数据如表 1 所示:

从表 1 的气体流量的实际幅值和拟合幅值的误差可以看出,涡街信号的幅值在理论值附近波动,且波动的范围一定,则幅频关系更一般的形式表达如下:
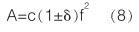
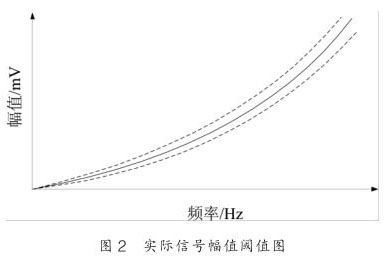
其中 c 为系数, δ 为相对误差限, 其示意图如图 2 所示,图中实线为幅频关系的理论拟合曲线, 而虚线为幅值波动的阈值曲线。根据实验的数据,涡街信号幅值波动的相对误差为 ±10% 。
3 实验仿真
本实验采用基于对管道振动信号进行分析, 其采样点数为2048 ,采用稀疏傅里叶变换对数据进行频谱分析。 如图 3 所示。
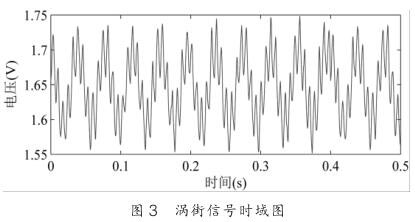
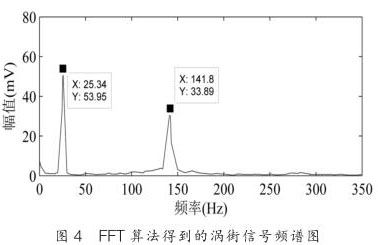
图 4 是用 FFT 算法对涡街时域信号分析后得到的频谱图,其中涡街信号频率为 141.8Hz ,振动噪声信号频率为 25.34Hz 。从图中可以看出,信号是稀疏的,稀疏度 K=2 。
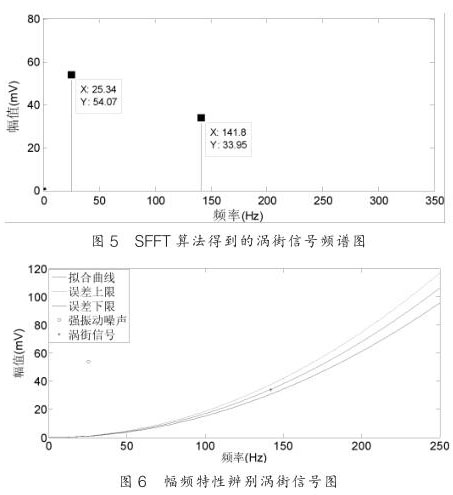
从图 5 可以看出 SFT 算法能够很好恢复,对涡街信号的频率恢复没有误差,而幅值的误差不超过 1% ,这对含有强振动噪声的涡街信号精确测量至关重要;图 6 是经 SFT 频谱分析所得到的数据通过幅频特性曲线来辨别是噪声信号还是涡街信号。通过幅频关系的信号处理方法可以从含有振动的混合信号中识别涡街信号,从而达到提高供暖蒸汽流量计抗振动性能的目的。
现在分析 SFT 算法的优越性。 基于哈希映射的稀疏傅里叶变换算法的时间复杂度为
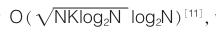
由前文可知 FFT 算法时间复杂度为 O ( Nlog 2 N )。 随着信号长度 N 的增长,两者的时间复杂度也会发生变化。 采用时间复杂度的数量级的比值来刻画这种变化:
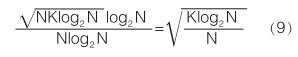
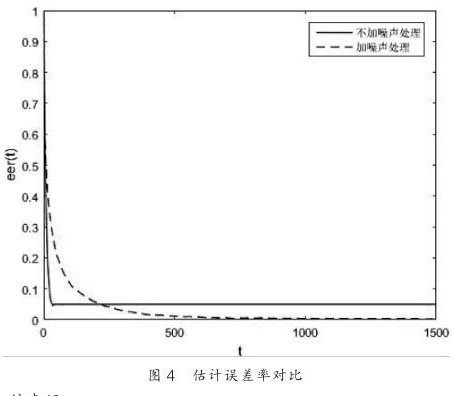
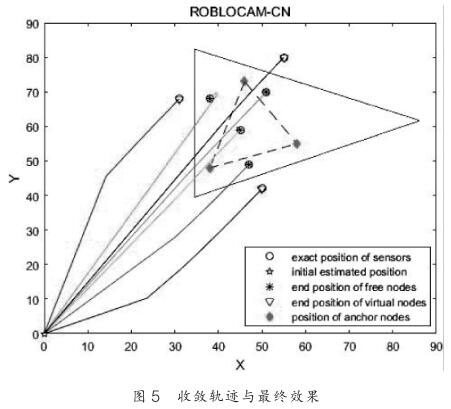
当 K=2 ,SFT 算法与 FFT 算法的时间复杂度的比值关系如图 7 所示。处理的 ROBLOCAM-CN 算法进行对比,其估计误差率 eer(t)对比效果如图 4 所示。从对比结果中可以看到,若不对通信噪声进行处理则各自由节点和墙的位置始终存在偏差 , 而 在ROBLOCAM-CN 算法下所有的自由节点与墙都迅速收敛至各自的精确位置,验证了本算法的有效性和鲁棒性。 各节点的收敛轨迹和*终的定位与环境构建效果如图 5 所示。
5 结束语
本文提出了一种噪声情形下新颖的室内定位与环境构建算法,该算法不需要无线传感器网络中的节点配备激光传感模块,只需要通过节点间的射频信号即可实现对周围环境的感知,为室内定位与环境构建技术提供了一种经济且可靠的解决方案。


